Search Tree
이진검색트리
Binary Search Tree
- 최대 두개의 자식노드
- 노드의 키 값은 왼쪽 자식 노드의 키 값보단 크고 오른쪽 자식의 키 값보단 작다.
- 이진 검색 트리에서의 삽입은 최악의 경우에도 이진트리가 균형이 잡혀있으면 시간복잡도는 O(logn).
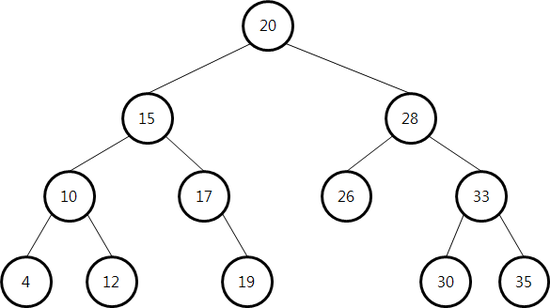
이진 검색 트리에서의 삭제
- 삭제하고자 하는 노드 r이 리프 노드인 경우 : 삭제
- 삭제하고자 하는 노드 r의 자식 노드 하나가 있는 경우 : r을 제거하고 r 자리에 r의 자식으로 대체
- 삭제하고자 하는 노드 r의 자식 노드 두개가 있는 경우 : r의 직후원소를 찾고 r을 데체
레드블랙트리
Red-Black Tree (RB-Tree)
1. 루트 노드는 블랙이다.
2. 노드가 레드이면 자식은 블랙이다.
3. 모든 리프(NIL)은 블랙이다 .(RB-TREE에서 말하는 리프노드는 NIL이다.
4. 루트 노드에서 임의의 리프 노드에 이르는 경로에서 만나는 블랙의 노드의 수는 같다.

특징
- 디스크의 접근 단위는 블랙(페이지 in OS)
- B-Tree는 디스크환경에서 사용하기 적합한 외부 다진검색트리이다.
- B-Tree는 균형잡힌(Balanced) 다진검색트리로, 다음의 성질을 만족한다.
- 루트를 제외한 모든 노드는 내림K/2~k개의 키를 갖는다.
- 모든 리프 노드는 같은 깊이를 가진다.(Balanced Tree이기 때문이다.)
B-Tree의 수행시간 분석
- 이진 검색 트리가 균형 = 밑이 2인 log n
- 다진 검색 트리가 균형 = 밑이 k인 log n
- B-Tree에서 임의 노드가 최대 d개의 자식을 가질 수 있다면 최소 내림[d/2]개의 자식을 가져야 한다.
- B-Tree의 검색 : O(logn) = 삽입(검색+오버플로우) = 삭제(직후원소 찾기 +언더플로우)
- B-Tree의 작업들은 점근적으로 O(log n)인데, 이진검색트리보다 상수인자가 상당히 작다.
다차원 검색
- 검색키가 두 개 이상의 필드로 이루어진 검색
e.g., 키(이름,학번)
1. KD-Tree
2. KDB- Tree
3. R-Tree
4. Greed file
'Algorithm' 카테고리의 다른 글
| 다중 계절성 시계열 예측 (2) | 2023.12.03 |
|---|---|
| Algorithm - [Stack & Queue] (0) | 2023.01.11 |
| Algorithm - [Asymptotic notation] (0) | 2023.01.10 |
| Algorithm - [Sort Algorithm] (0) | 2023.01.10 |