Algorithm - [Sort Algorithm]

Sort Algorithm

기초 정렬 알고리즘

 

1. 선택정렬

가장 작은 숫자를 구해 맨 왼쪽과 비교

수행시간 : (n-1) + (n-2) + ... + 2 + 1 = O(n^2)

장점

- n개의 원소에 대해서 n의 메모리를 할당하기 때문에 하나씩 정교하게 비교할 수 있다.

- 역순으로 정렬할 선택 정렬이 높은 효율을 보여준다.

 

단점

- 이미 정렬되어 있는 자료에 한개라도 자료가 추가 된다면 처음부터 재정렬하기 때문에 최악의 시간복잡도를 보일 수 있다.

 

 

Image from nox1004.tistory.com

 

2. 버블정렬

맨 왼쪽부터 오른쪽에 있는 숫자와 하나씩 비교

수행시간 : (n-1) + (n-2) + ... + 2 + 1 = O(n^2)

장점

- n개의 원소에 대해서 n의 메모리를 할당하기 때문에 하나씩 정교하게 비교할 수 있다.

 

단점

- 알고리즘 수행 시작할 때중간에 배열이 이미 정렬이 되어 있는데도 순환을 반복하는 한계가 존재

Image from https://wonjayk.tistory.com/218

 

3. 삽입정렬

맨 왼쪽부터 보면서 크기 순서가 맞지 않는 원소를 대소관계에 맞는 위치에 삽입

수행시간

1) Worst Case : (n-1) + (n-2) + ... + 2 + 1 = O(n^2)

2) Average Case :  Worst Case * 1/2 = O(n^2) - 50% 수준만 이동한다고 가정

3) Best Case : 만일 배열이 정렬되어 있으면, while Loop가 실행되지 않으니 O(n) 시간 소요

장점

- 버블정렬의 경우 정렬이 되어있어도 비교를 하게 되는데, 삽입정렬은 스킵해서 보다 효율적이다.

- 배열이 길이가 짧을 때 정렬하는 경우 버블정렬보다 효율적이다.

단점

- 배열의 길이가 길어질수록 비효율적이다.

- 여전히 최악의 경우 O(n^2)의 시간복잡도를 가진다.

Image from https://wonjayk.tistory.com/218

고급 정렬 알고리즘

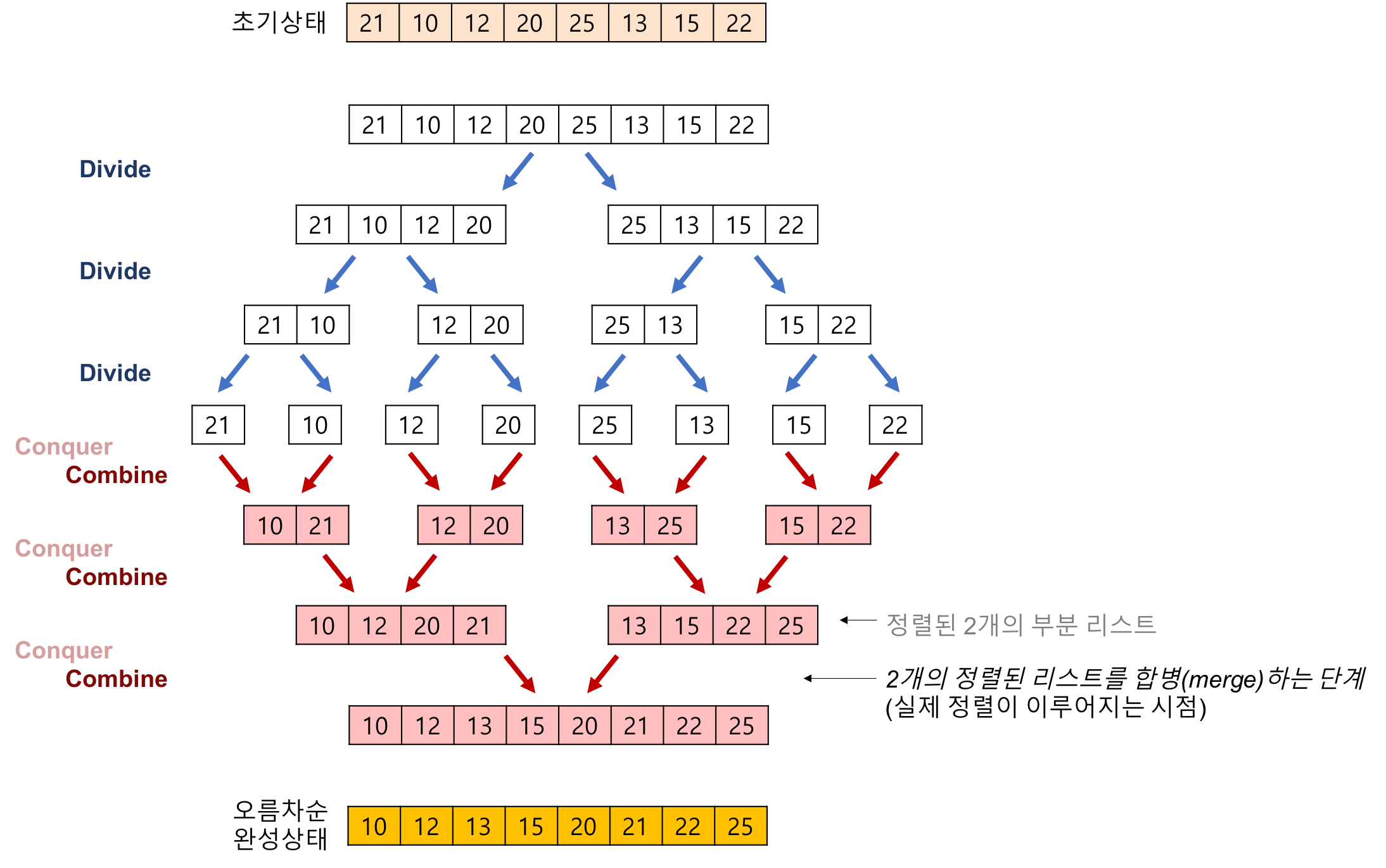
1. 병합정렬

주어진 문제를 절반으로 나눈 다음 각각을 재귀 호출로 풀어가는 방식이며 큰 문제를 작은 문제로 잘게 나누면 최종적으로 '종료조건'에 도달

이렇게 큰 문제를 작은 문제로 나누어서(분할) 푸는(정복) 방법을 '분할 정복' 이라고 한다

시간 복잡도 : O(n log n).

 

Image from gmlwjd9405.github.io

2. 퀵 정렬

기준 값을 설정하고 기준값보다 큰 값, 작은 값을 재귀함수를 활용하여 정렬

1) Worst Case : O(n^2)

2) Best Case :  O(n log n)

장점

- 앞서 소개한 알고리즘들보다 속도가 가장 빠르다.

- O(log n) 만큼의 메모리가 필요하다.

단점

- 정렬이 되어 있는 리스트에 대해서 불균형 분할 시 비효율적이다.

- 불균형을 방지하기 위해서 pivot 숫자를 중간값으로 설정해주어 단점을 보완할 수 있다.

Image from gmlwjd9405.github.io

 

 

3. 힙정렬

​

Image from Level Up coding

계산복잡도 총 정리

Image from find answer