DStory

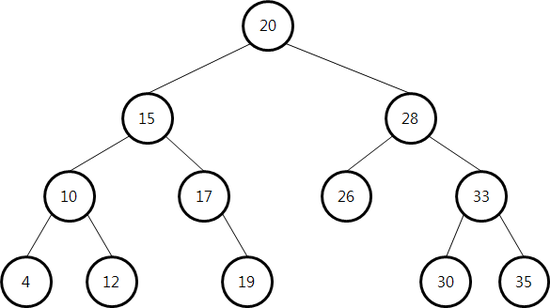
Search Tree 이진검색트리 Binary Search Tree - 최대 두개의 자식노드 - 노드의 키 값은 왼쪽 자식 노드의 키 값보단 크고 오른쪽 자식의 키 값보단 작다. - 이진 검색 트리에서의 삽입은 최악의 경우에도 이진트리가 균형이 잡혀있으면 시간복잡도는 O(logn). 이진 검색 트리에서의 삭제 - 삭제하고자 하는 노드 r이 리프 노드인 경우 : 삭제 - 삭제하고자 하는 노드 r의 자식 노드 하나가 있는 경우 : r을 제거하고 r 자리에 r의 자식으로 대체 - 삭제하고자 하는 노드 r의 자식 노드 두개가 있는 경우 : r의 직후원소를 찾고 r을 데체 ​ 레드블랙트리 Red-Black Tree (RB-Tree) 1. 루트 노드는 블랙이다. 2. 노드가 레드이면 자식은 블랙이다. 3. 모든 리..

Stack & Queue Stack '접시 쌓기' (Last In First Out) - push : 스택에 자료를 한개 집어 넣는 동작 pop : 스택 안에 있는 자료를 한 개 꺼내는 동작 ​- Stack이 비어있을 때 stack.pop -> stack underflow | Stack이 가득 찼을 때 stack.push -> stack overflow 시간 복잡도 가장 위에 있는 원소에 접근하기 때문에 접근, 삽입, 삭제의 시간복잡도는 O(1) 예 - 재귀 알고리즘 - 괄호검사, 후위 연산법, 문자열 역순 - DFS(Depth First Search) Queue '줄 서기' (First In First Out) - enqueue : 큐에 자료를 한 개 집어 넣는 동작 dequeue : 큐 안에 있는 자..

Asymptotic notation 알고리즘의 수행 시간을 표기하기 위해, 필수적인 부분에 집중하고 불필요한 상세들을 무시한다. 예를 들어, f(n) = n^2 + 2n 일 때, 시간 복잡도는 n^2이라고 한다. n이 무한대로 가는 데에선 낮은 차수의 증가폭이 높은 차수의 증가폭을 넘지 못하기 때문이다. 점근법 표기법 상한 표기법 : Big- O 점근적 상한만 알고 있을 때 사용하며 기껏해야 f(n)의 비율로 증가하는 함수 e.g. 7n-2가 O(n)임을 증명하라. sol) Let. c>0 이고 n_0 >= 1 n = 7n-2를 만족하는 c, n_0가 존재하는가? ​-> c=7,n_0 = 1일때 존재한다. ​ 하한 표기법 : Big - Omega 점근적 하한만 알고 있을 때 사용하며 적어도 f(n)의 비..

Sort Algorithm 기초 정렬 알고리즘 1. 선택정렬 가장 작은 숫자를 구해 맨 왼쪽과 비교 수행시간 : (n-1) + (n-2) + ... + 2 + 1 = O(n^2) 더보기 장점 - n개의 원소에 대해서 n의 메모리를 할당하기 때문에 하나씩 정교하게 비교할 수 있다. - 역순으로 정렬할 선택 정렬이 높은 효율을 보여준다. 단점 - 이미 정렬되어 있는 자료에 한개라도 자료가 추가 된다면 처음부터 재정렬하기 때문에 최악의 시간복잡도를 보일 수 있다. 2. 버블정렬 맨 왼쪽부터 오른쪽에 있는 숫자와 하나씩 비교 수행시간 : (n-1) + (n-2) + ... + 2 + 1 = O(n^2) 더보기 장점 - n개의 원소에 대해서 n의 메모리를 할당하기 때문에 하나씩 정교하게 비교할 수 있다. 단점 -..

Algorithm - 문제 해결 절차를 체계적으로 기술한 것 (입력으로부터 출력을 만드는 과정 기술) ​ 바람직한 알고리즘 1. 명확성 2. 효율적 3. 간결성 알고리즘 입출력의 예 e.g.입력 : 100개의 변수 (배열) x[1].x[2] ...x[100] , 출력 : x[1], x[2], ...x[100] 중 최대값 maxScore(x[], n) { x[1,...n]의 값을 차례때로 보면서 최대값을 계산; return 위에서 찾은 최대값; } 알고리즘 공부의 목적 1. 특정한 문제를 해결하기 위한 알고리즘 습득 2. 체계적 생각 훈련 - 문제자체를 해결하는 알고리즘 학습 - 그 과정에 깃든 '생각하는 방법' 배우는게 중요 3. 미래에 다른 문제를 해결하는 생각의 빌딩블록 제공 - 지적 추상회의 레벨 ..